Rekursion

Som vi har sett många gånger tidigare kan funktioner anropa andra funktioner. Till exempel:

def hej(namn : str):
    print("Hejsan,", namn)

def hej_flera(namn : str, ganger : int):
    for i in range(ganger):
        hej(namn)

En funktion kan också anropa sig själv, men vi som programmerare måste vara försiktiga när vi gör det. Det är lätt att hamna i en oändlig loop av funktionsanrop, precis som vi hamnade i en oändlig loop av upprepningar med while-loopar om vi utelämnade lämpliga brytvillkor. Så om man försöker anropa en hej-funktion med följande definition

def hej(namn : str):
    print("Hejsan,", namn)
    hej(namn)

skulle skapa ett nytt sort av fel:

Vad betyder rekursion?

Den rekursion som nämns i felet ovan innebär att man definierar något i termer av sig självt. I programmeringssammanhang handlar det oftast om en funktion som anropar sig själv. För att detta ska fungera utan att orsaka oändliga loopar måste de argument som skickas till funktionen ändras varje gång, så att de nästlade funktionsanropen slutar vid något skede. Grundprincipen här är densamma som i while-loopar: det måste alltid finnas ett stoppvillkor av något slag, och det villkoret måste utlösas vid någon tidpunkt i exekveringen.

Låt oss ta en titt på en enkel funktion som lägger till nollor i en lista så länge det finns färre än 10 objekt i listan. Den här gången använder vi dock inte en loop. Om villkoret ännu inte är uppfyllt anropar funktionen sig själv

def fyll_lista(tal: list):
    """ Lägger till föremål till listan ifall listans längd är kortare än 10 """
    if len(tal) < 10:
        tal.append(0)
        # anropa funktionen igen
        fyll_lista(tal)


if __name__ == "__main__":
    test = [1,2,3,4]
    fyll_lista(test)
    print(test)

Denna funktionalitet kunde lika väl bli uppnådd genom en vanlig while-loop:

def fyll_lista(tal: list):
    """ Lägger till föremål till listan ifall listans längd är kortare än 10 """
    while len(tal) < 10:
        tal.append(0)

if __name__ == "__main__":
    test = [1,2,3,4]
    fyll_lista(test)
    print(test)

Det mer traditionella iterativa tillvägagångssättet ger ett kortare program som förmodligen också är lättare att förstå. Med den rekursiva versionen är det inte lika tydligt att vi under hela processen arbetar med exakt samma lista. Så är det dock och därför fungerar den rekursiva funktionen lika bra.

Rekursion och returvärden

Rekursiva funktioner kan också ha returvärden. I de senaste avsnitten har vi arbetat med fakultettal, så låt oss skriva en rekursiv fakultetfunktion:

def fakultet(n: int):
    """ Funktionen räknar ut fakulteten n! för n>= 0 """
    if n < 2:
        # Fakulteten av 0 och 1 är 1
        return 1

    # anropa funktionen igen
    return n * fakultet(n - 1)

if __name__ == "__main__":
    # Testar
    for i in range(1, 7):
        print(f"Fakulteten av {i} är {fakultet(i)}")

Om parametern för den rekursiva faktoriella funktionen är 0 eller 1, returnerar funktionen 1, eftersom det är så faktoriell operation definieras. I alla andra fall returnerar funktionen värdet n * fakultet(n - 1), vilket är värdet av dess parameter n multiplicerat med returvärdet av funktionsanropet fakultet(n - 1).

Det avgörande här är att funktionsdefinitionen innehåller ett stoppvillkor. Om detta uppfylls avslutas rekursionen. I det här fallet är villkoret n < 2. Vi vet att det kommer att nås så småningom, eftersom det värde som skickas som argument till funktionen minskas med ett på varje nivå i rekursionen.

Visualiseringsverktyget kan vara till stor hjälp när det gäller att förstå rekursiva program.

Exemplet ovan skulle kanske bli lite tydligare om vi använde oss av hjälpvariabler:

def fakultet(n: int):
    if n < 2:
        return 1

    forra_talets_fakultet = fakultet(n - 1)
    fakultet_nu = n * forra_talets_fakultet
    return fakultet_nu

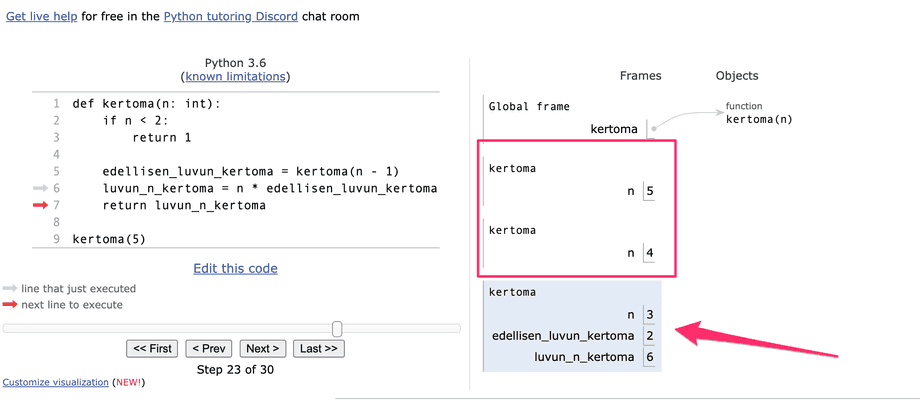
fakultet(5)

Ta en titt på hurvisualiseringsverktyget visar hur rekursionen fortskrider.

Visualiseringsverktyget har en liten finess i hur det hanterar anropsstacken, eftersom den verkar "växa" nedåt. Vanligtvis avbildas anropsstaplar som just staplar, där de nya anropen placeras överst. I visualiseringsverktyget är det aktiva funktionsanropet det skuggade blocket längst ner, som har sina egna kopior av de variabler som syns.

När den rekursiva faktorfunktionen anropas byggs anropsstapeln upp tills den gräns som utgörs av n < 2 nås. Då återkommer det sista funktionsanropet i stacken med ett värde - det är 1, eftersom n nu är mindre än 2. Detta återkomstvärde skickas till det föregående funktionsanropet i stacken, där det används för att beräkna det funktionsanropets återkomstvärde, och så vidare tillbaka ut ur stacken.

Returvärdet för varje funktionsanrop lagras i hjälpvariabeln fakultet_nu. Gå igenom visualiseringen noggrant tills du förstår vad som händer i varje steg, och var särskilt uppmärksam på det värde som returneras i varje steg.

Låt oss ta en titt på ett annat vanligt rekursivt exempel: Fibonacci-talen. I en Fibonacci-sekvens är varje tal summan av de två föregående talen. De två första talen definieras här som 1 och 1, och sekvensen börjar då så här: 1, 1, 2, 3, 5, 8, 13, 21, 34.

def fibonacci(n: int):
    """ Funktionen returnerar det n:e talet i Fibonaccis talföljd """

    if n <= 2:
        # de första två är ettor
        return 1

    # Alla andra tal blir summan av de två föregående talen
    return fibonacci(n - 1) + fibonacci(n - 2)

# Testar att allting fungerar
if __name__ == "__main__":
    for i in range(1, 11):
        print(f"Fibonaccis {i}. tal är {fibonacci(i)}")

Den här gången är stoppvillkoret att parametern är mindre än eller lika med 2, eftersom hela sekvensen definieras från de två första siffrorna och framåt, och vi definierade de två första siffrorna som lika med 1.

Hur fungerar då den här funktionen i praktiken?

Om funktionen anropas med 1 eller 2 som argument returnerar den 1, vilket dikteras av villkoret n <= 2.

Om argumentet är 3 eller större returnerar funktionen värdet av fibonacci(n - 1) + fibonacci(n - 2). Om argumentet är exakt 3 är detta värde lika med fibonacci(2) + fibonacci(1), och vi vet redan resultatet av båda dessa från föregående steg. 1 + 1 är lika med 2, som alltså är det tredje talet i Fibonacci-sekvensen.

Om argumentet är 4 är returvärdet fibonacci(3) + fibonacci(2), som vi nu vet är 2 + 1, vilket är lika med 3.

Om argumentet är 5 är returvärdet fibonacci(4) + fibonacci(3), vilket vi nu vet är 3 + 2, vilket är lika med 5.

Och så vidare, och så vidare.

Vi kan i varje steg verifiera att funktionen ger rätt resultat, vilket ofta är tillräckligt i grundläggande programmeringsuppgifter. Den formella verifierbarheten av algoritmer är ett ämne för mer avancerade kurser, till exempel Data Structures and Algorithms.

Binär sökning

I en binär sökning har vi en sorterad lista med objekt och vi försöker hitta ett visst objekt i den. Ordningen på objekten kan till exempel vara siffror från minst till störst, eller strängar från alfabetiskt först till sist. Sorteringsmetoden spelar ingen roll, så länge den är känd och relevant för det objekt som vi försöker hitta.

Tanken med en binär sökning är att alltid titta på objektet i mitten av listan. Vi har då tre möjliga scenarier. Om objektet i mitten är

• det vi letar efter: vi kan returnera en indikation på att vi hittade objektet
• mindre än det vi letar efter: vi kan göra om sökningen i den större halvan av listan
• större än den vi letar efter: vi kan göra om sökningen i den mindre halvan av listan.

Om listan är tom kan vi fastställa att objektet inte hittades och returnera en indikation på det.

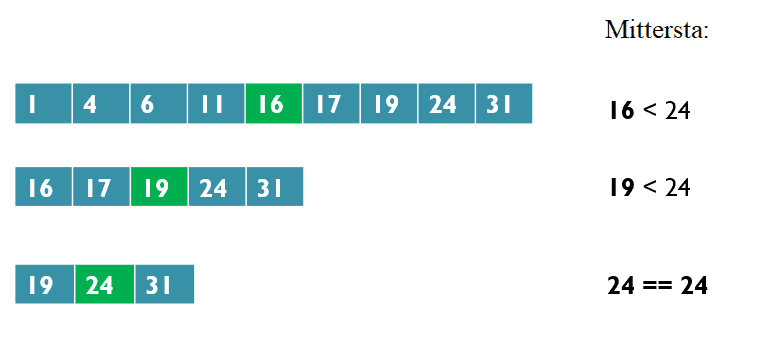
I följande bild kan vi se hur en binär sökning fortskrider när den letar efter talet 24:

Här är en rekursiv algoritm för en binär sökning:

def binarsokning(lista: list, foremal: int, vanster : int, hoger : int):
    """ Funktionen returnerar True ifall föremålet finns i listan, annars False """
    # Om sökfältet är tomt hittas inget föremål
    if vanster > hoger:
        return False

    # Kalkylerar mitten av sökområdet
    mitten = (vanster+hoger)//2

    # Ifall föremålet hittas i mitten
    if lista[mitten] == foremal:
        return True

    # Ifall föremålet är större, sök andra halvan
    if lista[mitten] < foremal:
        return binarsokning(lista, foremal, mitten+1, hoger)
    # Annars måste föremålet vara mindre, sök mindre halvan
    else:
        return binarsokning(lista, foremal, vanster, mitten-1)


if __name__ == "__main__":
    # Testar
    lista = [1, 2, 4, 5, 7, 8, 11, 13, 14, 18]
    print(binarsokning(lista, 2, 0, len(lista)-1))
    print(binarsokning(lista, 13, 0, len(lista)-1))
    print(binarsokning(lista, 6, 0, len(lista)-1))
    print(binarsokning(lista, 15, 0, len(lista)-1))

Funktionen binar_sokning tar fyra argument: mållistan, det objekt som söks samt vänster och höger kant på sökområdet. När funktionen anropas första gången täcker sökområdet hela mållistan. Den vänstra kanten ligger på index 0 och den högra kanten ligger på index len(lista)-1. Funktionen beräknar det centrala indexet och kontrollerar den positionen på listan. Antingen har objektet hittats eller så fortsätter sökningen till den mindre eller större halvan av mållistan.

Låt oss jämföra detta med en enkel linjär sökning. Vid en linjär sökning är sökområdet från början och framåt, tills antingen objektet hittas eller sökområdet tar slut. Antalet steg som behövs för att täcka hela sökområdet växer linjärt i samma takt som sökområdets storlek. Varje söksteg täcker endast en sökkandidat från början av sökområdet. Låt oss anta att det sökta objektet inte hittas. Om sökområdet är en miljon objekt långt måste vi ta en miljon söksteg för att försäkra oss om att objektet inte finns i sökområdet.

Vid en binär sökning växer däremot antalet steg som behövs logaritmiskt. Låt oss återigen anta att det sökta objektet inte hittas. Sökområdet halveras för varje steg, eftersom vi vet att objektet antingen är mindre eller större än den aktuella sökkandidaten i mitten. 2 gånger 20 (2^20) är redan långt över 1 miljon, så det tar som mest 20 steg att täcka hela sökområdet med en binär sökning. När vi har att göra med sorterade sökområden, vilket ofta är fallet när vi har att göra med datorer och material som ska bearbetas automatiskt, är en binär sökning alltså mycket effektivare än en linjär sökning.

Se dina poäng genom att klicka på cirkeln nere till höger av sidan.