Fler exempel på rekursion

De verkliga fördelarna med rekursion blir uppenbara när vi stöter på problem där iterativa lösningar är svåra att skriva. Låt oss ta en titt på binära träd, till exempel. Ett binärt träd är en förgrenad struktur där vi har noder och vid varje nod förgrenar sig strukturen, som mest, i två underordnade grenar med egna noder. Ett binärt träd skulle då kunna se ut så här (datavetenskap betraktas ofta som en gren av naturvetenskapen, men vår förståelse av träd är lite upp och ner, som du kommer att märka):

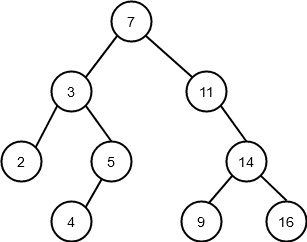
Binära träd bör åtminstone teoretiskt sett vara lätta att hantera rekursivt: om vi vill utföra någon operation på varje nod i trädet behöver vår algoritm helt enkelt

1. Behandla den aktuella noden
2. Anropa sig själv på barnnoden till vänster
3. Anropa sig själv på barnnoden till höger

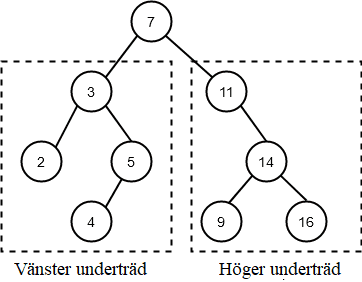
Som du kan se på bilden ovan är både de vänstra och högra "underträden" fullfjädrade binära träd i sig, och den enda nod som lämnas utanför de rekursiva anropen är den överordnade noden, som bearbetas i steg 1 innan funktionen anropas rekursivt. På så sätt kan vi vara säkra på att varje nod har besökts exakt en gång när funktionen är klar.

En iterativ version av en binär trädtraversering skulle vara mycket mer komplicerad, eftersom vi på något sätt skulle behöva hålla reda på alla noder som vi redan har besökt. Samma principer gäller för alla beräkningsbara trädstrukturer, inte bara binära.

Ett binärt träd är också lätt att modellera i Python-kod. Vi behöver bara skriva en klassdefinition för en enda nod. Den har ett värdeattribut och attribut för de vänstra och högra underordnade noderna:

class Nod:
    """ Klassen representerar en enkel nod i ett binärt träd """
    def __init__(self, varde, vanster_barn:'Nod' = None, hoger_barn:'Nod' = None):
        self.varde = varde
        self.vanster_barn = vanster_barn
        self.hoger_barn = hoger_barn

Låt oss anta att vi vill modellera följande träd:

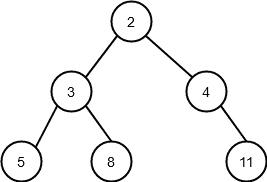
Vi kunde uppnå detta med följande kod:

if __name__ == "__main__":
    trad = Nod(2)

    trad.vanster_barn = Nod(3)
    trad.vanster_barn.vanster_barn = Nod(5)
    trad.vanster_barn.hoger_barn = Nod(8)

    trad.hoger_barn = Nod(4)
    trad.hoger_barn.hoger_barn = Nod(11)

Algoritmer för rekursiva binära träd

Låt oss först ta en titt på en algoritm som skriver ut alla noder i ett binärt träd en efter en. I de följande exemplen kommer vi att arbeta med det binära träd som definieras ovan.

Argumentet till utskriftsfunktionen är rotnoden i det binära trädet. Detta är noden högst upp i vår illustration ovan. Alla andra noder är barn till den här noden:

def skriv_ut_noder(rot: Nod):
    print(rot.varde)

    if rot.vanster_barn is not None:
        skriv_ut_noder(rot.vanster_barn)

    if rot.hoger_barn is not None:
        skriv_ut_noder(rot.hoger_barn)

Funktionen skriver ut värdet på den nod som skickas som argument och anropar sedan sig själv på de vänstra och högra underordnade noderna, förutsatt att noderna är definierade. Det här är en mycket enkel algoritm, men den går på ett effektivt och tillförlitligt sätt igenom alla noder i trädet, oavsett trädets storlek. Avgörande är att ingen nod besöks två gånger. Varje värde skrivs bara ut en gång.

Om vi skickar rotnoden trad i det binära trädet som illustreras ovan som ett argument till funktionen, skriver den ut

Som du kan se av ordningen på noderna i utskriften rör sig algoritmen först längs trädets "vänstra ben" ner till botten, och därifrån går den igenom de andra noderna i ordning.

På samma sätt kan vi skriva en algoritm för att beräkna summan av alla de värden som finns lagrade i trädets noder:

def nodernas_summa(rot: Nod):
    summa = rot.varde

    if rot.vanster_barn is not None:
        summa += nodernas_summa(rot.vanster_barn)

    if rot.hoger_barn is not None:
        summa += nodernas_summa(rot.hoger_barn)

    return summa

Variabeln summa initieras till att vara lika med värdet för den aktuella noden. Värdet i variabeln ökas sedan genom rekursiva anrop till nodens summor i det vänstra och högra underordnade trädet (först kontrolleras naturligtvis att de finns). Detta resultat returneras sedan.

Sorterat binärt träd

Ett binärt träd är särskilt användbart när noderna är sorterade på ett visst sätt. Det gör att det går snabbt och effektivt att hitta noder i trädet.

Låt oss ta en titt på ett träd som är sorterat på följande sätt: det vänstra barnet till varje nod är mindre än själva noden och det högra barnet är på motsvarande sätt större.

Nu kan vi skriva en rekursiv algoritm för att söka efter noder. Idén är mycket lik den binära sökningen från föregående avsnitt: om den aktuella noden är den nod vi letar efter, returnera True. Annars fortsätter vi rekursivt med antingen det vänstra eller det högra underordnade trädet. Om noden inte är definierad returneras False.

def sok_nod(rot: Nod, varde):
    if rot is None:
        return False

    if varde == rot.varde:
        return True

    if varde > rot.varde:
        return sok_nod(rot.hoger_barn, varde)

    return sok_nod(rot.vanster_barn, varde)

Besök till tiden innan rekursion

Låt oss avsluta denna del av materialet med en lite större övning som koncentrerar sig på objektorienterade programmeringsprinciper. Vi rekommenderar inte att du använder rekursion i denna serie av uppgifter, men tekniker för list comprehension kommer att vara användbara.

Svara slutligen på en snabb enkät:

Se dina poäng genom att klicka på cirkeln nere till höger av sidan.